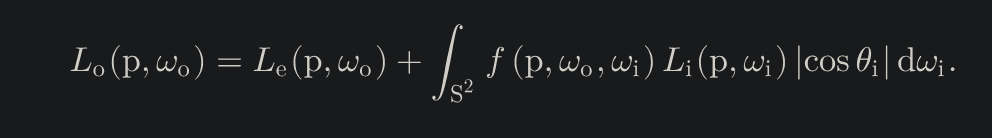Floating Orb
Red Hallway
Glass Ball on Table
Wall Blocks and Mirrors
Using OpenGL and C++, I made a Monte Carlo Pathtracer that runs on the GPU. A lot of the implementation details come from the PBR Book. The pathtracer renders a realistic scene by simulating light using the light transport equation, an expression written below that models light.
Since we can't solve this integral, we must approximate it on the computer using lots of samples of our integrand and then do a weighted average to get the integral result. We can make the samples that we take random, but biased towards directions that will likely have a lot of light energy in order to make our weighted average more accurate with less samples. This is called Monte Carlo estimation. There are different options - called integration schemes - for how we can bias the samples and how we can accumulate light energy. This project supports Naive Integration, Direct Light Integration, Multiple Importance Sampling Integration, and Full Light Integration.
With this integration scheme, we bounce tons of rays randomly through the scene. Only rays that happen to eventually hit a light contribute energy. This integration scheme takes a long time to converge to a clean image because it takes a lot of samples that don't contribute any energy because they don't hit a light.
Cornell Box
With this integration scheme, we bounce tons of rays through the scene, but once a ray comes out from the camera and hits the environment, we make sure it'll only bounce to the light. By doing this, most rays we send will hit a light and contribute energy after only 1 bounce. This integration scheme converges very quickly because we get more light in less time, but we lose the global illumination we'd get from multiple bounces.
Cornell Box with Two Lights
Cornell Box with Point Light
In order to get an accurate weighted average of light, we always want to bias our samples towards directions where there's a lot of light energy. However, the directions where a lot of light energy comes from depends on both an object's material and the light environment around it. In Naive Integration, we only biased our samples towards the normal of the surface because Lambert's law causes bounced light energy to get more intense closer to the normal. In Direct Light Integration we bias our incoming light vector samples towards the visible lights. Naive Integration biases based on the material and Direct Lighting biases based on the lights.
They're both usually okay but they fail when the aspect they don't take into account is important.
Naive Integration
Direct Lighting Integration
MIS Integration
As shown in the pictures, Naive Integration fails for tiny lights because it doesn't bias the samples towards the tiny lights so most of its samples miss the light. Direct Lighting fails when specular surfaces sample large lights because it doesn't bias the samples towards the thin lobe of directions that will actually let light bounce through. Multiple Importance Sampling takes two samples - one using the sampling method seen in Naive Integration (BSDF sampling) and one using Direct Lighting sampling - and uses a balance heuristic to decide the weighting of each sample. It combines the strengths of Naive and Direct Lighting and results in the most convergent render.
This integration scheme aims to get the fast convergence of Direct Lighting and MIS alongside the global illumination of Naive Integration. To do this, we bounce tons of rays randomly throughout the scene like in Naive Integration, but for each ray bounce, we send two additional rays that correspond to the BSDF and light samples of MIS. These two rays contribute energy. Through this scheme, we have global illumination from rays bouncing around the scene multiple times, but we also have fast convergence times because we accumulate a lot of important energy quickly because we accumulate energy on each ray bounce instead of only getting light when the ray ends at a light. To test the final pathtracer, I made some custom scenes, most of which can be seen at the top of this page.
Cornell Box
Mirrors and Blocks
Infinite Mirrors